Les graphes dans Normastic

Dans l’objectif de contribuer à l’émergence de nouvelles collaborations au sein de la fédération et au delà, un premier état des lieux des différentes variations de graphes et leurs usages dans la fédération a été réalisé afin de souligner complémentarités et différences dans la définition et l’usage de ces graphes. Sur une durée d’un an environ nous avons rencontré les chercheurs identifiés comme “représentants” d’une variation pour qu’ils présentent informellement leur travaux au cours d’un entretien. Le fruit de ces échanges est disponibles en intégralité dans un rapport et la journée du 13 octobre 2022 a été l’occasion de présenter aux membres de Normastic cette synthèse. La Figure 1 résume les approches identifiées qui sont détaillées par la suite et cite quelques applications transverses à ces approches.

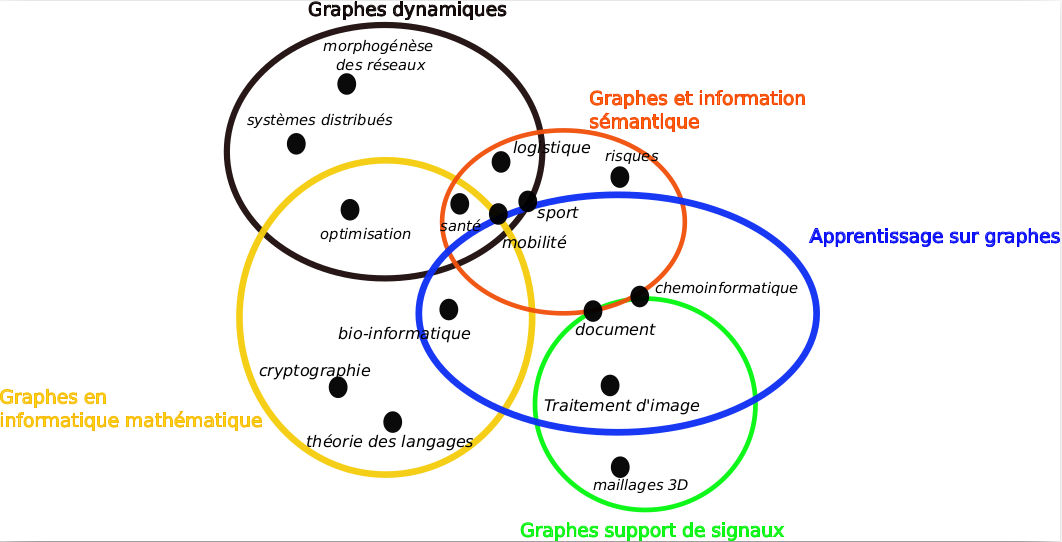
Les approches

Apprentissage sur graphes

L’analyse d’ensembles de graphes doit traiter une multitude de graphes, chaque graphe étant affecté d’une propriété (une classe ou une valeur réelle). L’activité de recherche consiste à définir des méthodes permettant de prédire la valeur d’un graphe inconnu à partir d’une base d’apprentissage de couples (graphe, propriété). Ce genre de problématique est classiquement résolu soit par des méthodes de fouille de données, soit par des méthodes d’apprentissage machine. Chaque approche recouvre bien sur plusieurs problématiques scientifiques. Les tailles des graphes incriminés sont généralement petites (une dizaine de sommets) à moyennes (quelques centaines).

Principales problématiques scientifiques

Fouille de données sur graphes Dans cette problématique, on doit manipuler un ensemble de graphes (codant généralement des molécules) divisé entre des graphes vérifiant une certaine propriété et des graphes ne la vérifiant pas. L’objet de la fouille de données va être de trouver des sous graphes fortement présents dans les graphes vérifiant la propriété et faiblement présent dans ceux ne la vérifiant pas. Dans le cadre de la recherche de médicaments, ces sous graphes sont appelés des pharmacophores. En fonction de la taille des ensembles envisagés, cette recherche peut produire des milliers ou des centaines de milliers de pharmacophores potentiels. Cet ensemble est ensuite filtré (par exemple grâce à la notion de sous-graphe) afin d’extraire un ensemble réduit de pharmacophores qui pourront être étudiés plus avant par un biologiste.

Métriques sur graphes L’essence de l’apprentissage machine est d’affecter une propriété à un objet inconnu à partir des propriétés d’objets supposés proches de celui-ci. Ceci passe donc nécessairement par la définition d’une métrique sur l’ensemble des objets (qui sont ici des graphes). La distance d’édition est une métrique historique dans l’espace des graphes. Celle-ci est liée à la notion de chemin d’édition (Figure 1). Un chemin d’édition entre deux graphes G1 et G2 permet de transformer G1 en G2 à l’aide de suppression/insertion de sommets ou d’arêtes ainsi que de changement de label (valeur) de sommets ou d’arêtes. Chaque opération élémentaire d’un chemin d’édition peut être affectée d’un coût, ce qui permet de définir le coût d’un chemin d’édition comme la somme de ses coûts élémentaires. La notion de distance d’édition se définit alors simplement comme le plus court chemin (ou la transformation la moins coûteuses) entre deux graphes. Le GREYC et le LITIS ont contribué de nombreuses fois à cette problématique soit séparément soit en collaboration.

 

Par exemple, de 2017 à 2019 le GREYC et le LITIS ont participé au projet régional AGAC regroupant le GREYC, le LITIS, le COBRA, le LCMT et le CERMN. Dans le cadre de ce projet un algorithme de calcul de graphe médian a été développé. Ce projet a également permis de jeter les bases d’un projet ANR portant sur les réseaux de neurones sur graphes(voir infra). Les méthodes à noyaux sur graphes permettent, comme la distance d’édition, de définir une métrique sur l’espace des graphes. Toutefois, à la différence de la distance d’édition, la métrique obtenue peut être combinée avec l’ensemble des méthodes à noyaux (la métrique de la distance d’édition n’est pas définie positive) Ceci permet de combiner ces noyaux avec l’ensemble des méthodes à noyaux définies en apprentissage machine (SVM, KPCA,. . .). On peut ainsi classifier des graphes, calculer l’axe principal de variations d’un ensemble de graphes ainsi que de nombreuses autres opérations jusqu’à présent restreintes aux données vectorielles. Le GREYC et le LITIS ont mené des travaux dans ce domaine. Les deux principaux domaines d’applications visés ont été la reconnaissance de formes (au sens shape) [82, 42] et la chémoinformatique [44, 46]. Bien que très efficaces, les méthodes à noyaux sur graphes fournissent généralement des résultats difficilement interprétables par un expert. L’équipe APP du LITIS travaille sur ce problème en cherchant à calculer la pré-image d’un ensemble de graphes. Il s’agit dans ce cas d’expliciter un graphe dont on ne connaît (via les noyaux) que les similarités avec les graphes d’un jeu de données (Figure 2). La technique utilisée et proche d’un calcul de graphe médian et combine des méthodes à noyaux et la distance d’édition. Dans le cadre d’une classification non supervisée, ces travaux permettent par exemple, d’expliciter les graphes codant le centre de chacune des classes obtenues.

 

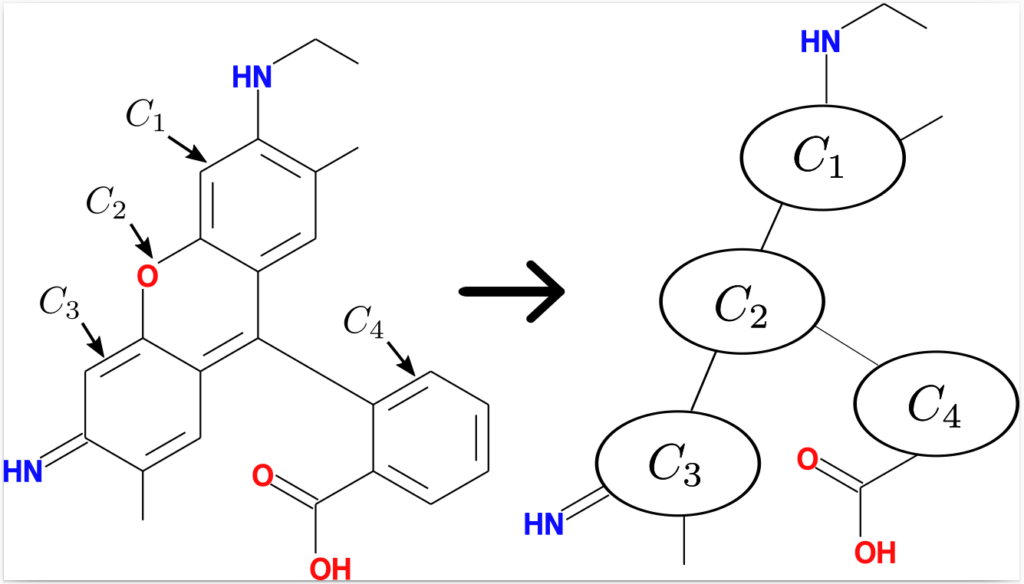
Réseaux de neurones sur graphes Dans le cadre du projet AGAC (voir distance d’édition), le LITIS s’est intéressé aux méthodes de réseaux de neurones sur graphes et plus précisément aux méthodes de convolution sur graphes. De cette étude à débouché une théorie permettant d’unifier les deux grandes familles de convolution sur graphes (spectrales et spatiales) et de pointer leurs limites [11, 76]. Suite au projet AGAC, le GREYC et le LITIS ont monté avec le laboratoire LIFAT de Tours un projet ANR (CodeGNN) qui a été accepté et est actuellement en cours. Les principaux domaines d’applications de ces travaux sont la bio et chémo informatique ainsi que l’étude des réseaux sociaux.

 

Traitement du signal sur graphes

On considère ici que chaque objet est codé par un sommet. Les poids des arêtes reliant ces sommets codent la similarité entre les objets (et donc la métrique définie sur l’espace codé par le graphe). Les arêtes du graphe peuvent être dirigées permettant ainsi de rendre la métrique non symétrique. Cette approche connue sous le nom de Traitement du signal sur graphe permet de traiter des ensembles d’objets de grandes dimensions et peut se décomposer en plusieurs sous domaines.

Principales problématiques scientifiques

Régularisation adaptative de signaux Dans cette problématique, la valeur des sommets est considérée comme un signal sur le graphe qu’il convient de régulariser en fonction de la métrique définie par les poids des arêtes. Le gradient de la fonction le long d’une arête, peut être interprété comme une dérivée partielle de la fonction et se calcule à partir des valeurs de la fonction sur deux sommets adjacents, du poids de l’arête reliant ces sommets et de l’ensemble des poids des arêtes incidentes aux deux sommets. Cette notion de gradient permet d’introduire la notion de régularisation qui se formalise comme la minimisation d’une fonctionnelle avec un terme de régularisation (dépendant du gradient) et une attache aux données.

 

Morphologie mathématique sur graphes L’introduction du gradient sur graphe permet d’introduire d’autres opérateurs tels que la divergence et le p-Laplacien. L’ensemble de ces opérateurs permet de considérer de nombreux problèmes définis dans le cas continue comme la solution d’une équation aux dérivées partielles. On parle dans le cas des graphes d’équations aux différences partielles. Les opérateurs de morphologie mathématique, à commencer par l’érosion et la dilatation, peuvent être définis comme la solution d’une équation différentielle non linéaire [26]. Ce pont entre morphologie mathématique et calcul différentiel permet de définir des opérateurs morphologique sur graphes via la notion de gradient.

Contours actifs sur graphes La définition d’opérateurs différentiels sur graphes permet d’adapter l’équation Eikonale qui est la base des méthodes type Level set de segmentation d’images. Son extension aux graphes permet donc de segmenter des données beaucoup moins structurées (Figure 3) ou de segmenter des images en introduisant des métriques non locales via des arêtes reliant des pixels distants.

Ce thème a pour objet principal d’étude l’analyse et le contrôle des réseaux d’interaction. Cette notion peut être en partie représentée par des graphes, auxquels s’ajoute une dimension temporelle qui permet de capturer la dynamique des réseaux. Ces graphes incluant l’évolution de réseaux portent de multiples noms dans la littérature : time-varying graphs[32], evolving graphs[19], dynamic networks[30], temporal networks[52], en fonction de leur domaine d’application d’origine. Si dans ce thème les sommets du graphes représentent souvent des objets, les arêtes en revanche représentent des interactions au sens large et non spécifiquement la similarité entre chaque objet. Les types de graphes peuvent être divers (orientés/non orientés, éventuellement valués). La taille des données ici représente quelques milliers à quelques dizaines de milliers de sommets et des séquences de quelques milliers d’étapes.

Principales problématiques scientifiques

Analyse des réseaux complexes et dynamiques L’objectif est de comprendre la génèse des réseaux d’interactions et de leurs structures (morphogénèse), et à la simuler à partir de modèles utilisant les graphes dynamiques. Il s’agit également de caractériser l’émergence de propriétés globales sur ces réseaux. A titre d’exemple les travaux [84, 83] abordent les aspects computationnels de la morphogénèse de réseaux complexes, en proposant un modèle général, capable de simuler leur formation. Les réseaux sont générés sous l’influence de contraintes qui s’expriment par l’intermédiaire d’un champ vectoriel qui est déterminé à l’aide d’un système de réaction-diffusion. Un modèle de Gray-Scott produisant une grande variété de motifs dynamiques est utilisé. Le champ vectoriel obtenu contrôle la géométrie et le taux de croissance du réseau construit qui rétroagit sur le processus de réaction diffusion.

Algorithmes d’optimisation Cet axe a pour but de répondre à des problèmes portant sur des systèmes complexes réels et pouvant s’exprimer comme des problèmes d’optimisation. Les méthodes utilisées relèvent de la recherche opérationnelle, programmation mathématique, metaheuristiques et algorithmes classiques sur les graphes, revisités pour satisfaire les exigences dues à la dynamicité et parfois à la nature distribuée des systèmes. A titre d’exemple, des travaux [87, 86] s’intéressent à la notion de connectivité dans les graphes dynamiques. Un graphe non orienté est défini sur un intervalle de temps fini et discret. Les arcs peuvent apparaître ou disparaître pendant l’intervalle de temps. Le premier objectif de ce travail est d’étendre la notion de composante connexe aux graphes dynamiques d’une manière nouvelle (Figure 4). Les composantes connexes persistantes sont définis par leur taille, correspondant au nombre de sommets, et leur longueur, correspondant au nombre de pas de temps consécutifs sur lesquels ils sont présents. Le deuxième objectif de ce travail est de développer un algorithme calculant les plus grandes (en termes de taille et de longueur) composantes connexes persistantes dans un graphe dynamique. L’algorithme PICCNIC (PersIstent Connected CompoNent InCremental Algorithm) est un algorithme polynomial en temps de complexité minimale.

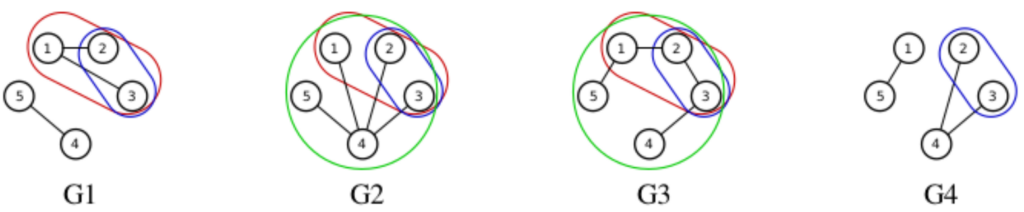
Algorithmique des systèmes distribués L’objectif est ici de proposer des algorithmes permettant de piloter ces systèmes en garantissant certaines propriétés liées à la connectivité, la sécurité, l’économie d’énergie, le maintien de structures géométriques. Il s’agit notamment de permettre le vol d’une formation autonome de drones uniquement guidés par leurs perceptions respectives et leurs interactions respectives, sans nécessiter l’intervention d’un guidage centralisé. Au delà du challenge technologique, le projet fait appel aux notions d’algorithmiques distribuées et à la modélisation par graphes dynamiques. Dans [47] par exemple, les auteurs s’intéressent à l’alignement autonome de robots sans communication ni information de placement. Seule la vision des robots est utilisée pour évaluer les positions angulaires des voisins.

Graphes et information sémantique

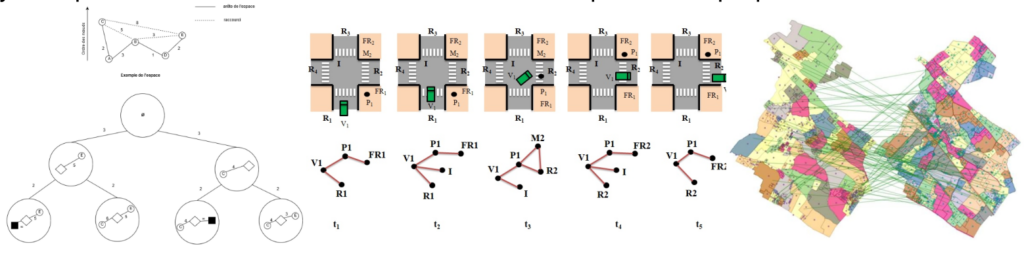
Ici le graphe a vocation a représenter la réalité le plus fidèlement possible sans tomber dans l’écueil d’une modélisation à une échelle trop fine. Le graphe n’est pas seulement un couple de sommets et d’arêtes, il dispose aussi d’information sémantique lui permettant de capturer les caractéristiques du monde réel, spécifiques au domaine applicatif pour lequel il est défini. En cela ce thème se distingue de celui couvert dans les Graphes Dynamiques, a fortiori sur l’aspect qualitatif de l’information. Tout type de graphe peut-être choisi et adapté (simple ou non, orienté ou non, hyper-graphe, multi- niveaux, statique, dynamique etc). Tout comme dans les Graphes Dynamiques, l’interdisciplinarité est au coeur de ce domaine, mais ici un focus fort (qui correspond également à une des problématiques de recherche de ce thème) est la définition du modèle de graphe sémantique qui sera en mesure de répondre au problème posé. Ce modèle devant potentiellement aussi prendre en compte d’autres contraintes plus bas niveau comme l’espace mémoire utilisé (ce qui a un impact sur sa définition, Figure 5 à gauche). Les autres problématiques de recherche portent sur les traitements opérés sur ces graphes qui peuvent être assez divers, mais souvent en lien avec la similarité entre graphes ou le matching de sous-graphes ainsi que la recherche de patterns (potentiellement dynamique). Il est souvent nécessaire d’adapter les définitions d’algorithmes ou de métriques classiques définis sur des graphes statiques simples à d’autres types de graphes (e.g. hyper-graphes, multi-graphe, bi-graph). Les méthodes de résolution sous-jacentes sont essentiellement algorithmiques et sont communes aux méthodes décrites dans l’approche Graphes Dynamiques, partie algorithmes d’optimisation. Toutefois, l’un des verrous de ce thème est la prise en compte de la dimension sémantique dans ces algorithmes. La taille des données peut varier mais ne concerne pas de grande masse de données. Par ailleurs, la recherche de solutions pour un nombre restreint de données est aussi l’un des challenges de cette thématique.

Principales problématiques scientifiques

Définition du modèle de graphe L’aspect modélisation est en soit pour ce thème une problématique scientifique. La définition du graphe dans sa structure est une première étape qui consiste à rechercher le type de graphe le plus approprié pour représenter la réalité du problème posé. Des graphes multi-échelles [74] aux hypergraphes en passant par des graphes simples, l’idée est de percevoir les caractéristiques permettant par la suite de répondre au mieux à la problématique initialement posée. A cette structure s’ajoute la composante sémantique qui permet d’enrichir l’information contenue dans le modèle au travers de valuation quantitative et/ou qualitative (un focus privilégié est fait sur ce deuxième aspect) des arêtes et des sommets. Les traitements pourront éventuellement s’abstraire de la sémantique pour des approches purement structurelles, ou au contraire en tenir compte. Souvent il s’agit de deux étapes distinctes. De récents travaux ont suggéré la possibilité de lier ces graphes sémantiques à des graphes de connaissances dans des modèles plus complexes afin d’aller plus loin dans l’enrichissement du contenu et permettre l’inférence de solutions [39].

Recherche de patterns (statique ou dynamique) Ce traitement opéré sur les graphes sémantiques a pour objectif de rechercher des patterns spécifiques (e.g. zones de vulnérabilités dans un réseau viaire,situations particulières dans le trafic routier[69, 71] (Figure 5 au centre), changements spatiaux dans des parcellaires historiques, enclenchements dans un match de handball). Ce qui est appelé « pattern » est un sous-graphe qui peut être défini sur un graphe statique ou dynamique. Par graphe dynamique on entend plutôt ici séquence de graphes statiques, même si des réflexions ont pu être menées sur des graphes dynamiques agrégés. Le matching de graphe est aussi un enjeu sous-jacent dans le sens où il est parfois nécessaire de faire le lien entre des données à des temps différents avant de pouvoir appliquer des algorithmes de recherche de patterns dynamiques (Figure 5 à droite).

Définition et calcul de métriques sur graphe L’analyse des graphes sémantiques conduit à l’utilisation et/ou à la définition de métriques sur graphes permettant de répondre aux problématiques pour lesquelles ces graphes ont été définis. Par exemple, la comparaison de graphes est souvent au coeur de beaucoup d’applications et nécessite la définition de métriques spécifiques sur ces graphes. S’il est possible d’appliquer des métriques classiques, il faut souvent les adapter aux types de graphes utilisés qui ne correspondent pas aux hypothèses initiales de ces métriques classiques. Par ailleurs, l’objectif est aussi d’en définir de nouvelles qui permettent d’être plus précis dans cette comparaison. Cette thématique pourrait être rapprochée de ce qui se fait dans l’approche Analyse d’ensembles de Graphes mais sur des ensembles de graphes beaucoup plus restreint et avec des méthodologies différentes. L’adaptation des métriques aux aspects dynamiques comme dans l’approche Graphes Dynamiques est aussi une problématique potentielle de ce thème.

Graphes en informatique mathématique

En informatique mathématique, on étudie les classes de complexité algorithmique des problèmes associés, et on en déduit le cas échéant de l’algorithmique efficace. Les graphes étudiés peuvent être des graphes définis usuellement (graphe nus) ou des graphes nus auxquels on ajoute des informations (graphes décorés). On peut utiliser les graphes comme structures de données ou supports de modélisation. Les contraintes de modélisation ou l’algorithmique incitent souvent à restreindre la famille d’objets étudiée. On peut aussi chercher à transposer des propriétés connues sur les graphes classiques à des extensions de graphes (graphes dynamiques, hypergraphes [37]).

Principales problématiques scientifiques

Étude des graphes nus. Un graphe est habituellement défini comme un couple (E, V), avec E un ensemble de sommets et V un ensemble d’arêtes. Cette définition peut être déclinée par exemple en changeant le type des ensembles utilisés ou en imposant des propriétés sur V. Ce sont les graphes nus. Voici quelques exemples de graphes nus contraints :

• un graphe cordal est obtenu par ajouts successifs de sommets, de telle sorte qu’à chaque ajout, le voisinage du sommet dans le graphe forme une clique. Ils apparaissent dans de nombreux domaines, en algorithmique paramétrée (via la notion de treewidth), en statistique (réseaux bayésiens) ou en bio-informatique (phylogénie parfaite) ;
• les graphes de degré borné (degré = nombre de sommets voisins), où l’on étudie [41], par exemple, la conjecture de Bruce-Reed [75] qui relie, dans le cas connexe, le degré d’un graphe et la taille minimale d’un ensemble dominant (un ensemble D est dominant si tout sommet du complémentaire est voisin d’un sommet de D).

On se pose d’abord des problèmes d’optimisation combinatoire (coloration, domination, ensembles indépendants) et on étudie les algorithmes correspondant : même si beaucoup de ces problèmes restent NP-difficiles (même sur ces sous-classes), divers algorithmes donnent des solutions satisfaisantes dans ces cas usuels, et on veut analyser leur complexité sur ces sous-classes. On réfléchit aussi à la liaison entre les propriétés qui définissent la sous-classe et l’estimation des principaux paramètres du graphe (dans le pire des cas ou en moyenne) ; c’est par exemple le cas de la conjecture de Bruce-Reed. On se pose aussi des questions liées au comptage et à la génération aléatoire de graphes d’une sous-classe donnée, comme dans le cas des graphes cordaux, par exemple.

Graphes nus supports de problématiques ou reliés à des algorithmes. Il s’agit ici d’utiliser les graphes nus comme support d’une problématique : la résolution d’un problème est ramenée à un problème de graphes, ou la caractérisation d’un système (algébrique par exemple) à une caractérisation sur les graphes. Voici quelques exemples :

• les monoïdes de traces [40] sont des objets algébriques particulièrement utilisés dans l’étude théorique des programmes concurrents ou dans lesquels certaines instructions peuvent commuter. La relation de commutation (ou de non commutation) dans l’étude des monoïdes de traces peut naturellement être représentée par un graphe ; des sous-familles permettent de caractériser et étudier des classes particulières de monoïdes de traces ayant de bonnes propriétés.
• le problème « Permutation-Équivalence de codes » [62] est essentiel dans la classification des codes et intervient en particulier en cryptanalyse. En supposant qu’on dispose d’un algorithme décidant si deux graphes pondérés non dirigés sont isomorphes, la permutation-équivalence des codes sur un corps arbitraire est décidable [13] de manière déterministe (sous hypothèse).
• l’ensemble des versions successives d’un logiciel, avec les liens de parenté entre les versions, définissent un graphe orienté. L’algorithme git-bisect [34] (utilisé dans le logiciel de développement collaboratif git) cherche un point de régression parmi les versions (une première version qui contient un bug) avec des méthodes proches de la recherche dichotomique. Il s’agit d’analyser finement la complexité de cet algorithme.

Graphes décorés comme structures de données. Quand on lui ajoute des attributs, le graphe devient une structure de données efficace pour organiser et stocker l’information ; elle se révèle donc essentielle dans beaucoup de cadres algorithmiques. Nous l’utilisons pour modéliser des processus, en algorithmique du texte et en bio-informatique. Il s’agit ici de définir des structures de données compactes et permettant d’opérer efficacement [48, 36] : ce sont des automates (oracle des facteurs [2], mais aussi d’autres automates de types variés [15]), des arbres (tries, suffix-tries), des DAG, parfois des graphes de de Bruijn [68]. L’algorithmique reliée permet de rechercher des motifs, corriger les erreurs dans le séquençage, de passer d’une structure à une autre, etc. . . Les applications sont nombreuses : l’exemple de la bio-informatique est développé ci-dessous dans les Domaines Applicatifs Phares.

Extensions possibles. On cherche aussi à étendre les problématiques bien maîtrisées sur les graphes à certaines de leurs généralisations (graphes dynamiques, hypergraphes). Pour les graphes dynamiques, c’est un lien fort avec l’approche Graphes Dynamiques et potentiellement l’approche Graphes et Information Sémantique. Pour les hypergraphes, le calcul de toutes les traverses minimales d’un hypergraphe est un problème qui apparaît dans de nombreux domaines, en particulier en fouille de données. On recherche un algorithme efficace qui résolve la question.

Quelques domaines applicatifs phares

Analyse de jeux de molécules

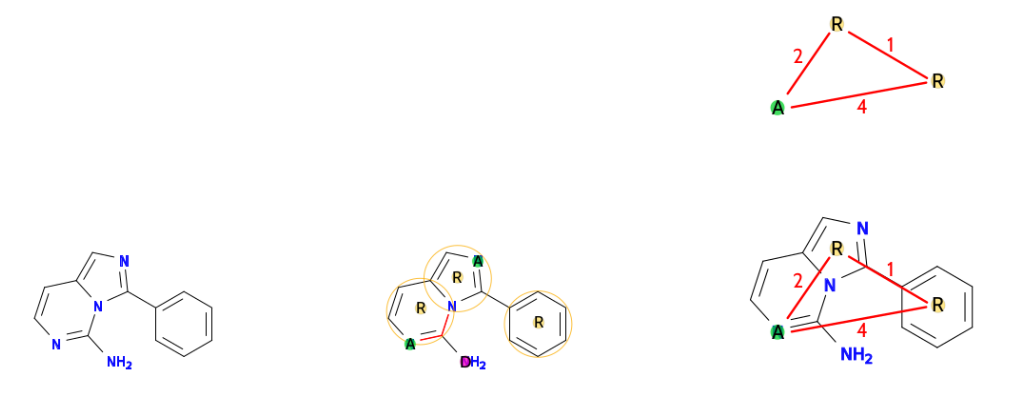
Les molécules se prêtent particulièrement bien à une représentation par graphes. En effet, un molécule peut, en première approche, être décrite par un ensemble d’atomes (carbone, oxygène,. . .) reliés par des liaisons (simple, double, triples, aromatiques,. . .). La prédiction des propriétés chimiques, physiques ou biologiques des molécules est un champs disciplinaire à part entière nommé la chémoinformatique. Notons que la prédiction de propriétés assez spécifiques des molécules peut requérir des modélisations par graphes plus haut niveau que les simples liaisons atomiques. C’est par exemple souvent le cas pour les propriétés biologiques. Une des clés pour analyser les propriétés curatives (ou plus simplement biologiques) des molécules consiste à générer des pharmacophores. On appelle ici pharmacophore un sous-graphe dont les occurrences dans le jeu de données satisfont certaines conditions exigées par l’analyse. La figure 7 donne un exemple d’occurrences de pharmacophore dans une molécule.
Ces conditions peuvent être des conditions exigeant un nombre minimum d’occurrences, une différence de fréquences selon les sous-groupes du jeu de données. Il résulte de la première étape un grand nombre de pharmacophores, plusieurs centaines de milliers. L’analyse de données s’appuie sur ces pharmacophores et sur les molécules qui les contiennent. Cette analyse est mixte : elle contient des traitements automatiques qui orientent des explorations manuelles du chimiste afin de découvrir des liens dans les résultats et de construire sa théorie chimique.

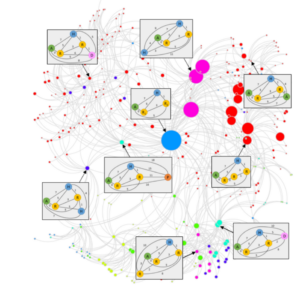
Ces explorations nécessitent de trouver une structure pour organiser les pharmacophores et les molécules. Dans ce but, il s’agit souvent de s’appuyer sur la relation d’inclusion, produisant ainsi des diagrammes de Hasse. Ces diagrammes sont de très grands graphes orientés donc chaque sommet représente un élément de l’analyse (un pharmacophore) et chaque arête une relation d’inclusion. La figure 8 montre un exemple de diagramme de Hasse.

Une autre approche, plus orientée apprentissage machine consiste à prédire les propriétés biologiques mais également physiques ou chimiques des molécules soit au travers de réseaux de neurones sur graphes soit à partir de mesures de similarité ou de distance entre les molécules. Dans ces derniers cas, on utilise soit des méthodes à noyaux soit la distance d’édition sur graphes.

Utilisation des graphes en bio-informatique

Les travaux développés en bio-informatique visent à rechercher, indexer et extraire des informations pertinentes notamment dans des données biologiques (génomes et expression des génomes). Dans ce but il s’agit de définir des structures de données qui minimisent l’espace mémoire et permettent des traitements efficaces (e.g. indexation, recherche de motifs).

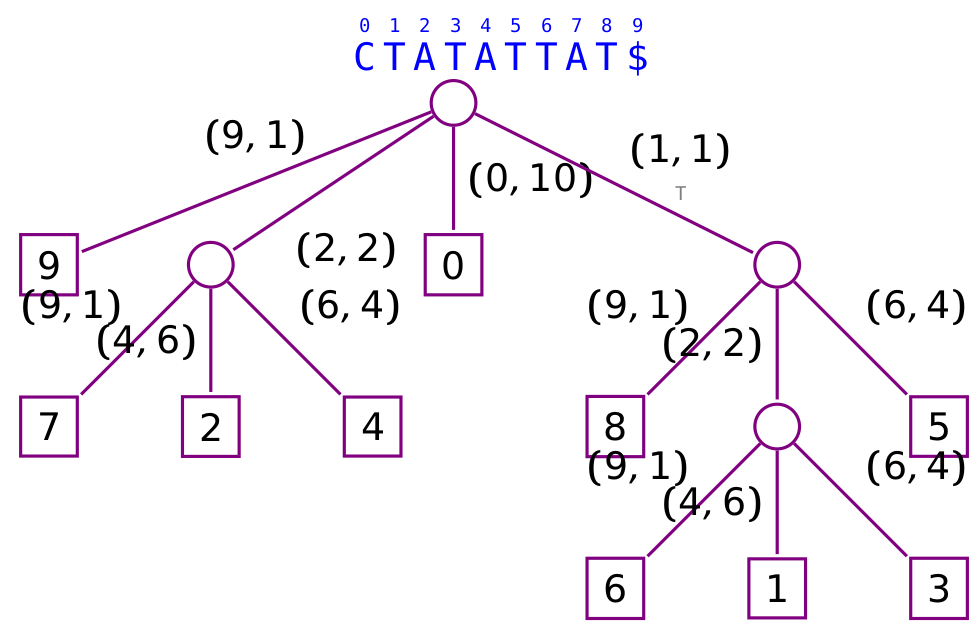
 Pour cela différents types de graphes sont utilisés, comme des arbres (e.g. arbre compact des suffixes, Figure 9). Cette structure s’avère encore trop gourmande en espace pour de longues séquences. Il existe plusieurs méthodes pour encore réduire l’espace nécessaire. L’une d’elle, l’oracle des facteurs [3] est un automate fini déterministe qui reconnait un peu plus que l’ensemble des facteurs d’une séquence. Par ailleurs, les génomes ne peuvent pas être séquencés en un seul morceau. Ils sont donc fragmentés, les fragments sont ensuite amplifiés et enfin séquencés. À l’aide des multiples copies des fragments générés il faut alors reconstruire le génome d’origine. Pour cela deux types de graphes sont principalement utilisés : les graphes de chevauchement et les graphes de de Bruijn [33]. Notons toutefois qu’à partir d’une certaine taille de données, les graphes ne sont plus la structure de donnée la plus pertinente. Des structures de données alternatives, souvent basées sur la transformée de Burrows-Wheeler permettent de remplacer avantageusement ces derniers.

Analyse d’évènements sportifs

L’analyse d’un jeu collectif (football, handball,. . .) se base principalement sur les positions relatives des joueurs, d’un éventuel ballon et leurs positions vis à vis du terrain. Tout ceci peut être modélisé par un graphe qui sera nécessairement dynamique du fait de l’évolution des positions des joueurs au cours du temps. Il s’agit dans ce cadre de détecter des motifs récurrents (au cours du temps) caractéristiques de réussites tactiques. Les sommets de tels graphes peuvent être simplement les différents éléments sus-cités ou un diagramme de Voronoï utilisant les positions des joueurs et du ballon comme centres (Figure 10). Les arêtes du graphe peuvent être valuées par une distance, une expérimentation sur la possibilité d’inclure des relations spatiales qualitatives a aussi été envisagée.

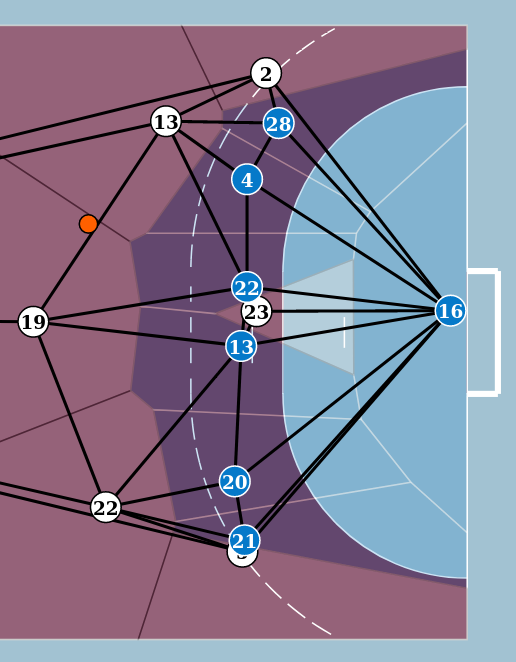
Logistique et mobilité

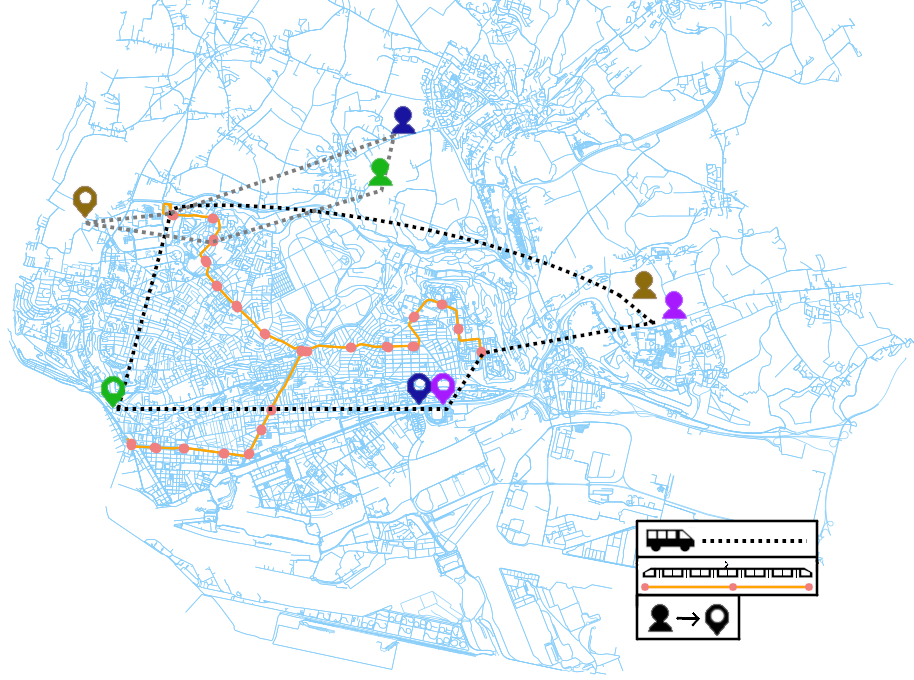
Les réseaux viaires se prêtent particulièrement à la modélisation par graphe. Différentes versions existent comme de prendre les intersections pour les sommets du graphe et les tronçons routier entre ces intersections pour les arêtes du graphe, la réciproque est aussi utilisée. Ces graphes peuvent tenir compte de l’orientation du réseau, de la présence de plusieurs voies (multi-graphe) etc. La valuation des arêtes peut par exemple représenter une distance, un temps de parcours, une vitesse… Ces réseaux peuvent être étudiés d’un point de vue statique ou dynamique (Figure 11). Dans ce second cas, on tient compte par exemple du déplacement des véhicules sur ce réseau. Les problématique de logistique, de gestion portuaire, détection de patterns de mobilité font partie des thèmes qui utilisent ce type de modélisation et peuvent être couplées à des simulations multi-agents.

Une tout autre type de modélisation par graphe peut également être utilisé, il s’agit de représenter les acteurs au sein de la gestion logistique d’un système comme les sommets d’un graphe statique, où les arêtes caractérisent les relations entre ces acteurs. L’objectif est ici de caractériser la gouvernance au sein d’une place portuaire et de pouvoir comparer plusieurs places portuaires par la comparaison des graphes sous-jacents.

Analyse de documents

Un document fait par des êtres humains est généralement fortement structuré, Cette structuration spatiale correspond à une structure logique ou sémantique sous-jacente. Le codage des relations physiques par un graphe permet donc indirectement de capturer de l’information sémantique (Figure 12).

Dans le cas de lettres ou de documents administratifs, les champs tels que l’adresse, l’objet, le destinataire, la présence de tableaux. . . peuvent être des éléments discriminants. La détection de ces éléments et leur mise en relation par un graphe permet une première indexation des documents. Notons, que malgré la numérisation, les administrations continuent à recevoir des centaines de milliers de courrier chaque jour.
De même, dans le cadre de l’analyse de plans, les éléments de ces plans (portes, tables, murs,. . .) peuvent être décomposés en plusieurs parties qui auront sensiblement les mêmes relations d’adjacence dans différents documents. Le codage de ces éléments par des graphes et la recherche de sous graphes dans les plans est une technique couramment utilisée pour détecter toutes les occurrences d’un ou plusieurs objets (e.x. une table contre un mur). Ce type de recherche se nomme du pattern spotting.
Enfin, dans le cadre de l’analyse de documents anciens, les images peintes ou dessinées présentent également une forte structure qui peut être utilisée, via un codage par graphe pour opérer du pattern spotting afin de détecter leur occurences dans des banques de documents.

Synthèse

Trois principaux courants émergent de cette réflexion : Graphes & Informatique Mathématique, Graphes & masse de données et Graphes dynamiques & sémantiques (Figure 13). L’idée est de les présenter au travers des complémentarités des approches qui les composent, et également de montrer les liens qui existent entre eux. Nous soulignerons aussi certaines différences car nous pensons qu’elles peuvent permettent de mieux cerner les différentes approches.

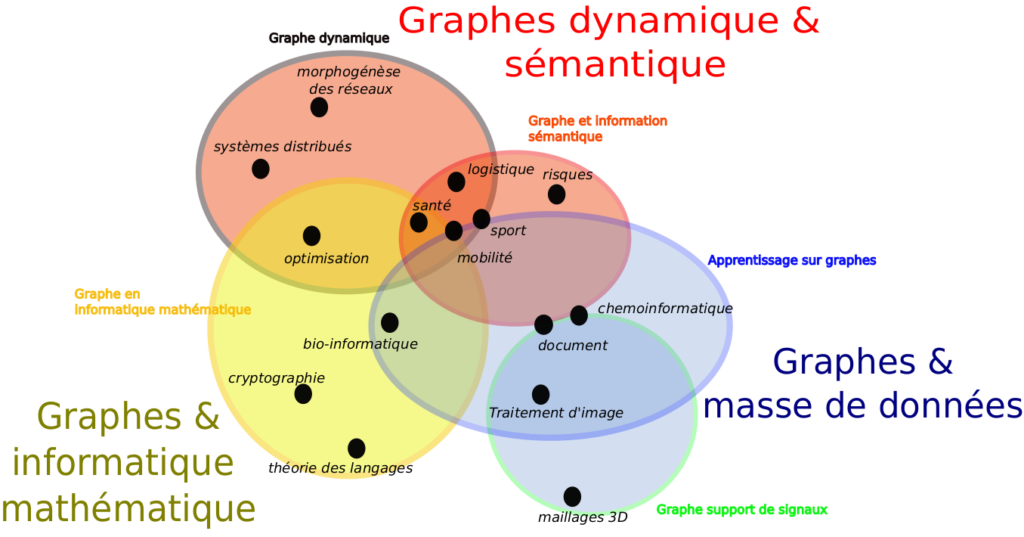
Les graphes dans NormaSTIC

L’interdisciplinarité est au coeur des enjeux de nombreux travaux, mais particulièrement en ce qui concerne les approches relatives aux Graphes dynamiques et sémantisés. Certains des verrous scientifiques (e.g. adaptation d’algorithmes/concepts sur des graphes statiques aux graphes dynamiques) et les stratégies de résolution sont proches et complémentaires (e.g. algorithmique sur graphe, optimisation). Si les Graphes sémantisés n’excluent pas de travailler sur des structures statiques, la dimension temporelle est très souvent nécessaire pour modéliser les phénomènes sur lesquels porteront les analyses, et en cela les Graphes Dynamiques sont d’un réel apport pour ces approches. Réciproquement, actuellement les Graphes Dynamiques utilisent très peu l’information sémantique pour valuer les graphes étudiés, a fortiori la dimension qualitative de cette information est sous-exploitée. Par ailleurs, de nombreuses applications (e.g. logistique, sport) sont d’ors et déjà sujets à des travaux communs ce qui démontre des liens forts entre ces deux visions des graphes.

Le courant des graphes dynamiques & sémantiques a régulièrement besoin de s’intéresser aux propriétés structurelles des graphes et à l’optimisation des algorithmes appliqués à ces graphes. Ces deux enjeux peuvent être adressés au courant graphes & informatique mathématique qui traite de problématiques complémentaires voire communes. Les graphes dynamiques & sémantiques ont aussi des besoins d’adaptation de métriques classiques sur des graphe qui peuvent être travaillés selon des points de vue très généraux (sans application) comme par exemple des calcul de densité sur des hypergraphes orientés. D’autres défis, comme l’adaptation de la notion de chemin dans les Graphes Dynamiques ou d’autres problématiques de recherche opérationnelle peuvent accueillir l’expertise du courant graphes & informatique mathématique. Réciproquement, le courant des graphes dynamiques & sémantiques peut apporter d’autres sources d’applications que celles déjà traitées par les graphes & informatique mathématique (e.g. bioinformatique) et une autre vision méthodologique de l’approche des graphes. On note déjà des travaux communs entre ces deux courants (e.g. DyNet, stage NormaSTIC) mais le potentiel semble là pour aller plus loin dans cette démarche.

Des problématiques d’isomorphismes de graphes et de comparaison de graphes en général sont très présentes au sein du courant graphes & masses de données. Elles le sont aussi dans les approches précédemment décrites de manière plus ou moins transposables. L’approche Graphes et apprentissage et le courant graphes dynamiques & sémantiques peuvent aisément se comprendre autour de la comparaison de graphes (e.g. travaux en mobilité [70] en cours de soumission). Notamment dans le cadre de la recherche de patterns dans un graphe (potentiellement dynamique), la recherche d’occurences etc. Dans ce cadre, il serait intéressant de pouvoir tester les méthodes utilisées dans l’approche Graphes et apprentissage sous réserve du seuil critique de données nécessaires pour que ces méthodes fonctionnent. Par ailleurs, pour faire le lien avec le courant graphes & informatique mathématique, notons que de nombreuses méthodes de comparaison de graphes sont dérivées des algorithmes A∗ . D’autres formulations se basent soit sur de la programmation par contraintes, soit reformulent le problème comme un problème de minimisation en nombre entier sous contrainte. Par ailleurs, toutes les contraintes liées au temps de calcul, complexité, et au stockage de l’information, qui sont des problématiques adressées par le courant graphes & informatique mathématique sont au coeur des préoccupations des deux autres courants.

L’extension du Traitement du Signal sur Graphes fournit un support théorique aux convolutions ainsi qu’aux représentations multi-échelles de signaux sur graphes. Ces deux thématiques scientifiques sont au coeur des problématiques des réseaux de neurones sur graphes abordés dans Graphes et apprentissage. Il existe donc une voie de convergence entre ces deux approches combinant un monde de graphes (Graphes et apprentissage) et un monde codé par un graphe (Traitement du Signal sur Graphes). Les deux approches peuvent également converger autour de pré traitement à apporter aux graphes avant analyse. Il serait par exemple intéressant d’étudier des méthodes de segmentation de document à partir de graines en utilisant des équations aux différences partielles sur graphes.

Conclusion

L’étude de l’usage des graphes au sein de la fédération NormaSTIC a démontré l’existence de nombreuses activités allant de la théorie des graphes aux applications (bio-informatique, sport, document,….) en passant par l’étude de nombreux usages des graphes (traitement, classification, exploration,…). Le vivier graphe est donc riche au sein de NormaSTIC et les interactions que nous avons identifiées entre les différents axes sont extrêmement prometteuses tant d’un point de vue théorique qu’en termes de retombées applicatives.

Bibliographie

[1] A. V. Aho and M. J. Corasick. Efficient string matching : an aid to bibliographic search. Commun.
ACM, 18(6) :333–340, 1975.

[2] Cyril Allauzen, Maxime Crochemore, and Mathieu Raffinot. Factor oracle : A new structure for pattern matching. In Jan Pavelka, Gerard Tel, and Miroslav Bartosek, editors, SOFSEM ’99, Theory and Practice of Informatics, 26th Conference on Current Trends in Theory and Practice of Informatics, Milovy, Czech Republic, November 27 – December 4, 1999, Proceedings, volume 1725 of Lecture Notes in Computer Science, pages 295–310. Springer, 1999.

[3] Cyril Allauzen, Maxime Crochemore, and Mathieu Raffinot. Factor oracle : A new structure for pattern matching. In Jan Pavelka, Gerard Tel, and Miroslav Bartosek, editors, SOFSEM ’99, Theory and Practice of Informatics, 26th Conference on Current Trends in Theory and Practice of Informatics, Milovy, Czech Republic, November 27 – December 4, 1999, Proceedings, volume 1725 of Lecture Notes in Computer Science, pages 295–310. Springer, 1999.

[4] Amazigh Amrane and Nicolas Bedon. Logic and rational languages of scattered and countable
series-parallel posets. CoRR, abs/1912.10240, 2019.

[5] Amazigh Amrane and Nicolas Bedon. Logic and rational languages of scattered and countable series-parallel posets. In Carlos Martín-Vide, Alexander Okhotin, and Dana Shapira, editors, Language and Automata Theory and Applications – 13th International Conference, LATA 2019, St. Petersburg, Russia, March 26-29, 2019, Proceedings, volume 11417 of Lect. Notes in Comput. Sci., pages 275–287, St. Petersburg,Russian Federation, 2019. Springer.

[6] Amazigh Amrane and Nicolas Bedon. Equational theories of scattered and countable series-parallel
posets. In Nataša Jonoska and Dmytro Savchuk, editors, Developments in Language Theory, LNCS,pages 1–13, Cham, 2020. Springer International Publishing.

[7] Amazigh Amrane and Nicolas Bedon. Logic and rational languages of scattered and countable
series-parallel posets. Theoretical Computer Science, 809 :538–562, 2020.

[8] Gérard Assayag and Shlomo Dubnov. Using factor oracles for machine improvisation. Soft Comput.,
8(9) :604–610, 2004.

[9] László Babai. Graph isomorphism in quasipolynomial time. CoRR, abs/1512.03547, 2015.

[10] László Babai, Paolo Codenotti, Joshua A. Grochow, and Youming Qiao. Code Equivalence and Group
Isomorphism, pages 1395–1408. 2011.

[11] Muhammet Balcilar, Guillaume Renton, Pierre Héroux, Benoit Gaüzere, Sébastien Adam, and Paul
Honeine. Analyzing the expressive power of graph neural networks in a spectral perspective. In Proceedings of the International Conference on Learning Representations (ICLR), 2021.

[12] Magali Bardet, Julia Chaulet, Vlad Dragoi, Ayoub Otmani, and Jean-Pierre Tillich. Cryptanalysis
of the mceliece public key cryptosystem based on polar codes. In Tsuyoshi Takagi, editor, Post Quantum Cryptography, pages 118–143, Cham, 2016. Springer International Publishing.

[13] Magali Bardet, Ayoub Otmani, and Mohamed Saeed-Taha. Permutation code equivalence is not harder than graph isomorphism when hulls are trivial. In IEEE International Symposium on Information Theory, ISIT 2019, Paris, France, July 7–12, 2019, pages 2464–2468. IEEE, 2019

[14] Magali Bardet, Ayoub Otmani, and Mohamed Saeed-Taha. Permutation code equivalence is not harder than graph isomorphism when hulls are trivial. In IEEE International Symposium on Information Theory, ISIT 2019, Paris, France, July 7-12, 2019, pages 2464–2468. IEEE, 2019.

[15] Nicolas Bedon. Logic and branching automata. Logical Methods in Computer Sciences, 11(4 :2) :1–38, October 2015.

[16] Nicolas Bedon. Logic and branching automata. Logical Methods in Computer Sciences, 11(4 :2) :1–38, October 2015.

[17] Nicolas Bedon. Branching Automata and Pomset Automata. In Mikołaj Bojańczy and Chandra Chekuri, editors, 41st IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2021), volume 213 of Leibniz International Proceedings in Informatics (LIPIcs), pages 37 :1–37 :13, Dagstuhl, Germany, 2021. Schloss Dagstuhl – Leibniz-Zentrum für Informatik.

[18] Nicolas Bedon and Chloé Rispal. Series-parallel languages on scattered and countable posets.
Theoretical Computer Science, 412(22) :2356–2369, 2011.

[19] Sandeep Bhadra and Afonso Ferreira. Complexity of connected components in evolving graphs
and the computation of multicast trees in dynamic networks. In International Conference on Ad-Hoc Networks and Wireless, pages 259–270. Springer, 2003.

[20] David Blumenthal, Sébastien Bougleux, Johann Gamper, and Luc Brun. Gedlib : A c++ library for
graph edit distance computation. In Donatello Conte, Jean-Yves Ramel, and Pasquale Foggia, editors, 12th IAPR TC15 Workshop on Graph-Based Representation in Pattern Recognition (GbR), volume 11510 of LNCS, pages 14–24, Tours, June 2019. IAPR TC15, Springer.

[21] David B. Blumenthal, Nicolas Boria, Sébastien Bougleux, Luc Brun, Johann Gamper, and Benoit Gaüzère. Scalable generalized median graph estimation and its manifold use in bioinformatics, clustering, classification, and indexing. Information Systems, 100 :101766, 2021.

[22] Wieb Bosma, John Cannon, and Catherine Playoust. The magma algebra system i : The user language. Journal of Symbolic Computation, 24(3) :235–265, 1997.

[23] Sébastien Bougleux, Luc Brun, Vincenzo Carletti, Pasquale Foggia, Benoit Gaüzère, and Mario Vento. Graph edit distance as a quadratic assignment problem. Pattern Recognition Letters, 87 :38–46, 2017. Advances in Graph-based Pattern Recognition.

[24] Sébastien Bougleux, Benoit Gaüzère, David B. Blumenthal, and Luc Brun. Fast linear sum assignment with error-correction and no cost constraints. Pattern Recognition Letters, 134 :37–45, 2020.Applications of Graph-based Techniques to Pattern Recognition.

[25] Iliya G. Bouyukliev. About the code equivalence, pages 126–151. 2007.

[26] R.W. Brockett and P. Maragos. Evolution equations for continuous-scale morphological filtering.
IEEE Transactions on Signal Processing, 42(12) :3377–3386, 1994.

[27] Luc Brun, Benoit Gaüzère, Sébastien Bougleux, and Florian Yger. A new Sinkhorn algorithm with
Deletion and Insertion operations. Research report, GREYC, UMR 6072, November 2021.

[28] J. Richard Büchi. Transfinite automata recursions and weak second order theory of ordinals. In
Proc. Int. Congress Logic, Methodology, and Philosophy of Science (1964), pages 2–23, Jerusalem,1965. North-Holland Publ. Co. Invited address.

[29] J. Richard Büchi and Dirk Siefkes. The monadic second order theory of all countable ordinals, volume
328 of Lecture notes in mathematics. Springer, 1973.

[30] Binh-Minh Bui-Xuan, Afonso Ferreira, and Aubin Jarry. Computing shortest, fastest, and foremost journeys in dynamic networks. International Journal of Foundations of Computer Science,14(02) :267–285, 2003.

[31] R. Carmo, J. Donadelli, Y. Kohayakawa, and E. Laber. Searching in random partially ordered sets.
Theoret. Comput. Sci., 321(1) :41–57, 2004.

[32] Arnaud Casteigts, Paola Flocchini, Walter Quattrociocchi, and Nicola Santoro. Time-varying graphs and dynamic networks. International Journal of Parallel, Emergent and Distributed Systems, 27(5) :387–408, 2012.

[33] Bastien Cazaux, Thierry Lecroq, and Eric Rivals. Linking indexing data structures to de Bruijn
graphs : Construction and update. J. Comput. Syst. Sci., 104 :165–183, 2019.

[34] Christian Couder. Fighting regressions with git bisect. https://git-scm.com/docs/, git-bisect-lk2009, 2009.

[35] Bruno Courcelle and J. Engelfriet. Graph structure and monadic second-order logic, a language
theoretic approach. Cambridge university Press, 2011.

[36] Maxime Crochemore, Christophe Hancart, and Thierry Lecroq. Algorithms on strings. Cambridge
University Press, 2007.

[37] Julien David, Loïck Lhote, Arnaud Mary, and François Rioult. An average study of hypergraphs and
their minimal transversals. Theor. Comput. Sci., 596 :124–141, 2015.

[38] Julien David, Loïck Lhote, Arnaud Mary, and François Rioult. An average study of hypergraphs and
their minimal transversals. Theor. Comput. Sci., 596 :124–141, 2015.

[39] Géraldine Del Mondo, Peng Peng, Jérôme Gensel, Christophe Claramunt, and Feng Lu. Leveraging
spatio-temporal graphs and knowledge graphs : Perspectives in the field of maritime transportation. ISPRS International Journal of Geo-Information, 10(8), 2021.

[40] V Diekert and G Rozenberg. The Book of Traces. WORLD SCIENTIFIC, 1995.

[41] Paul Dorbec, Michael A. Henning, Mickael Montassier, and Justin Southey. Independent domination in cubic graphs. J. Graph Theory, 80(4) :329–349, 2015.

[42] François-Xavier Dupé. Restauration et reconnaissance des formes dans des images avec bruit de Poisson : application à l’analyse des neurones en microscopies de fluorescence. Theses, Université
de Caen, January 2010.

[43] Thomas Feulner. The automorphism groups of linear codes and canonical representatives of their
semilinear isometry classes. Advances in Mathematics of Communications, 3(4) :363–383, 2009.

[44] Benoit Gaüzère. Application des méthodes à noyaux sur graphes pour la prédiction des propriétés
des molécules. Theses, Université de Caen, November 2013.

[45] Benoit Ga »uz‘ere, Pierre-Anthony Grenier, Luc Brun, and Didier Villemin. Treelet kernel incorporating
cyclic, stereo and inter pattern information in chemoinformatics. Pattern Recognition, 48(2) :356–367, February 2015.

[46] Pierre-Anthony Grenier. Modélisation de la stéréochimie : une application à la chémoinformatique. Theses, Université de Caen Normandie, November 2015.

[47] Frédéric Guinand, François Guerin, and Mark Bastourous. Alignment of Three Robots without Communication nor Localization*. In 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), pages 647–654, Bari, Italy, October 2019. IEEE.

[48] John. E. Hopcroft, Rajeev Motwani, and Jeffrey. D. Ullman. Introduction to automata theory, languages, and computation. Pearson, 3 edition, 2006.

[49] Linlin Jia, Benoit Gaüzère, and Paul Honeine. A graph pre-image method based on graph edit distances. In Proceedings of IAPR Joint International Workshops on Statistical techniques in Pattern Recognition (SPR 2020) and Structural and Syntactic Pattern Recognition (SSPR 2020)., 2021.

[50] Tobias Kappé, Paul Brunet, Bas Luttik, Alexandra Silva, and Fabio Zanasi. Brzozowski goes concurrent – A Kleene theorem for pomset languages. In Proc. CONCUR 2017 : 28th International Conference on Concurrency Theory, volume 28, pages 21 :1–21 :15, 01 2017.

[51] Tobias Kappé, Paul Brunet, Bas Luttik, Alexandra Silva, and Fabio Zanasi. On series-parallel pomset
languages : Rationality, context-freeness and automata. Journal of Logical and Algebraic Methods in Programming, 103, 12 2018.

[52] David Kempe, Jon Kleinberg, and Amit Kumar. Connectivity and inference problems for temporal networks. Journal of Computer and System Sciences, 64(4) :820–842, 2002.

[53] Stephen C. Kleene. Representation of events in nerve nets and finite automata. In Shannon and McCarthy, editors, Automata studies, pages 3–41, Princeton, New Jersey, 1956. Princeton University Press.

[54] A. Lefebvre and T. Lecroq. Computing repeated factors with a factor oracle. In L. Brankovic and
J. Ryan, editors, Proceedings of the 11th Australasian Workshop On Combinatorial Algorithms, pages 145–158, Hunter Valley, Australia, 2000.

[55] Arnaud Lefebvre and Thierry Lecroq. Compror : On-line lossless data compression with a factor oracle. Inf. Process. Lett., 83(1) :1–6, 2002.

[56] Arnaud Lefebvre, Thierry Lecroq, Hélène Dauchel, and Joël Alexandre. Forrepeats : detects repeats on entire chromosomes and between genomes. Bioinform., 19(3) :319–326, 2003.

[57] J. Leon. Computing automorphism groups of error-correcting codes. IEEE Transactions on Information Theory, 28(3) :496–511, 1982.

[58] Kamal Lodaya and Pascal Weil. A Kleene iteration for parallelism. In V. Arvind and R. Ramanujam, editors, Foundations of Software Technology and Theoretical Computer Science, volume 1530 of Lect. Notes in Comput. Sci., pages 355–367. Springer-Verlag, 1998.

[59] Kamal Lodaya and Pascal Weil. Series-parallel posets : algebra, automata and languages. In M. Morvan, Ch. Meinel, and D. Krob, editors, STACS’98, volume 1373 of Lect. Notes in Comput. Sci., pages 555–565. Springer-Verlag, 1998.

[60] Kamal Lodaya and Pascal Weil. Series-parallel languages and the bounded-width property. Theoretical Computer Science, 237(1–2) :347–380, 2000.

[61] Camille Marchet, Pierre Morisse, Lolita Lecompte, Arnaud Lefebvre, Thierry Lecroq, Pierre Peterlongo, and Antoine Limasset. ELECTOR : evaluator for long reads correction methods. NAR Genomics and Bioinformatics, 2(1) :1–12, 2020.

[62] R. J. McEliece. A Public-Key Cryptosystem Based On Algebraic Coding Theory. Deep Space Network Progress Report, 44 :114–116, January 1978.

[63] R. J. McEliece. A Public-Key Cryptosystem Based On Algebraic Coding Theory. Deep Space Network Progress Report, 44 :114–116, January 1978.

[64] Brendan D. McKay and Adolfo Piperno. Practical graph isomorphism, ii. Journal of Symbolic Computation, 60 :94–112, 2014.

[65] Lorenz Minder and Amin Shokrollahi. Cryptanalysis of the sidelnikov cryptosystem. In Moni Naor, editor, Advances in Cryptology – EUROCRYPT 2007, pages 347–360, Berlin, Heidelberg, 2007. Springer Berlin eidelberg.

[66] P Morisse, C Marchet, A Limasset, T Lecroq, and A Lefebvre. Scalable long read self-correction and assembly polishing with multiple sequence alignment. Sci. Rep., 11(1) :761, 2021.

[67] Pierre Morisse, Thierry Lecroq, and Arnaud Lefebvre. Hybrid correction of highly noisy long reads using a variable-order de Bruijn graph. Bioinform., 34(24) :4213–4222, 2018.

[68] Pierre Morisse, Thierry Lecroq, and Arnaud Lefebvre. Hybrid correction of highly noisy long reads using a variable-order de Bruijn graph. Bioinform., 34(24) :4213–4222, 2018.

[69] Kamaldeep S Oberoi, Géraldine Del Mondo, Yohan Dupuis, and Pascal Vasseur. Towards a qualitative spatial model for road traffic in urban environment. In 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), pages 1724–1729. IEEE, Oct 2017.

[70] Kamaldeep Singh Oberoi. Spatio-temporal modeling of urban road traffic. Theses, Normandie Université, November 2019.

[71] Kamaldeep Singh Oberoi, Géraldine Del Mondo, Yohan Dupuis, and Pascal Vasseur. Modeling Road Traffic Takes Time. In 10th International Conference on Geographic Information Science (GIScience 2018), volume 114 of Leibniz International Proceedings in Informatics (LIPIcs), pages 52 :1–52 :7, Dagstuhl, Germany, 2018. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.

[72] Louise Penz. Interconnexion d’un système de transport point à point et d’un réseau de transport en commun (en cours). Theses, Université du Havre.

[73] E. Petrank and R.M. Roth. Is code equivalence easy to decide ? IEEE Transactions on Information Theory, 43(5) :1602–1604, 1997.

[74] Laura Pinson, Géraldine Del Mondo, and Pierrick Tranouez. Representation of interdependencies between urban networks by a multi-layer graph. In 14th International Conference on Spatial Information Theory (COSIT 2019), volume 142, Regensburg, Germany, Sep 2019. Sabine Timpf, Christoph Schlieder, Markus Kattenbeck, Bernd Ludwig, and Kathleen Stewart eds.

[75] Bruce Reed. Paths, stars and the number three. Combinatorics, Probability and Computing,5(3) :277–295, 1996.

[76] Guillaume Renton. Analyzing and improving graph neural networks. Theses, Normandie Université, July 2021.
[77] Mohamed Ahmed Saeed-Taha. Algebraic Approach for Code Equivalence. PhD thesis, Normandy University, 2017.

[78] N. Sendrier. Finding the permutation between equivalent linear codes : the support splitting algorithm. IEEE Transactions on Information Theory, 46(4) :1193–1203, 2000.

[79] Nicolas Sendrier. On the dimension of the hull. SIAM Journal on Discrete Mathematics, 10(2) :282–293, 1997.

[80] Nicolas Sendrier. Cryptosystèmes à clé publique basés sur les codes correcteurs d’erreurs. PhD thesis, Université Paris 6, 2002. Mémoire d’habilitation à diriger des recherches.

[81] Nicolas Sendrier and Dimitris E. Simos. The hardness of code equivalence over and its application to code-based cryptography. In Post-Quantum Cryptography, volume 7932 of Lect. Notes in Comput. Sci., pages 203–216. Springer, 2013.

[82] Frédéric Suard. Méthodes à noyaux pour la détection de piétons. Theses, INSA de Rouen, December 2006.

[83] Michele Tirico. Morphogenesis of complex networks. An application in urban growth. phdthesis, Normandie Université, 2020.

[84] Michele Tirico, Stefan Balev, Antoine Dutot, and Damien Olivier. Morphogenesis of complex networks : A reaction diffusion framework for spatial graphs. In Luca Maria Aiello, Chantal Cherifi,Hocine Cherifi, Renaud Lambiotte, Pietro Lió, and Luis M. Rocha, editors, Complex Networks and Their Applications VII, Studies in Computational Intelligence, pages 769–781. Springer International Publishing, 2019.

[85] Jacobo Valdes, Robert E. Tarjan, and Eugene L. Lawler. The recognition of series parallel digraphs. SIAM J. Comput., 11 :298–313, 1982.

[86] Mathilde Vernet. Modèles et algorithmes pour les graphes dynamiques. Theses, Normandie Université, October 2020.

[87] Mathilde Vernet, Yoann Pigné, and Éric Sanlaville. A study of connectivity on dynamic graphs :computing persistent connected components. 4OR, 2022.

[88] P. Weiner. Linear pattern matching algorithm. In Proceedings of the 14th Annual IEEE Symposium
on Switching and Automata Theory, pages 1–11, Washington, DC, 1973.